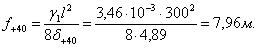Решение уравнения состояния провода на логарифмической линейке
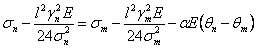 - уравнение состояния провода (основное расчетное уравнение).
- уравнение состояния провода (основное расчетное уравнение).
Это кубическое уравнение 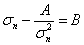 или
или 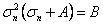 - решается чаще всего методом подбора на логарифмической линейке, (это раньше, сейчас, на ЭВМ, методом половинного деления и другими).
- решается чаще всего методом подбора на логарифмической линейке, (это раньше, сейчас, на ЭВМ, методом половинного деления и другими).
Расчет по этому уравнению можно проводить и для монометаллических и комбинированных проводов. Для комбинированных проводов в расчетное уравнение подставляются величины, характеризующие провод в целом (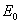 ;
; 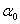 и другие).
и другие).
Таким образом, имея уравнение состояния провода, зная напряжения при «m»-ных условиях, мы можем найти напряжения в материале провода при любых атмосферных условиях.
Вопрос в том, какое напряжение является исходным. Отправной точкой будут являться допускаемые напряжения. При любых условиях напряжения в материале провода не должно быть больше допускаемой величины. Мы имеем три допускаемых напряжения, нужно определить которое нам нужно.
Три допускаемых напряжения (при наибольшей нагрузке, при низшей температуре и среднегодовой температуре) принимались до 1975 года для сталеалюминиевых проводов (высокое – при гололеде, ниже – при низшей температуре), для монометаллических проводов одинаковые. В 1975 году установлены допускаемые напряжения при низшей температуре такие же, как и при наибольшей нагрузке.
Решение на логарифмической линейке (К.П.Крюков, Б.П.Новгородцев. Конструкции и механический расчет линий электропередачи.)
Устанавливаем на нижней шкале предполагаемое значение искомого напряжения 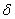 и подводим к этому значению начало или конец шкалы движка. На верхней неподвижной шкале получаем значение
и подводим к этому значению начало или конец шкалы движка. На верхней неподвижной шкале получаем значение 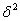 , которое надо умножить на
, которое надо умножить на 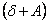 по верхней шкале движка; если значение произведения
по верхней шкале движка; если значение произведения 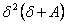 получается меньше, чем
получается меньше, чем 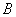 , то значение
, то значение 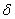 надо увеличить. Передвигаем движок и умножаем
надо увеличить. Передвигаем движок и умножаем 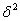 на новое значение
на новое значение 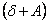 до тех пор, пока не получим произведение, равное
до тех пор, пока не получим произведение, равное 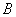 . После получения правильного произведения следует проверить, нет ли ошибки в разряде чисел.
. После получения правильного произведения следует проверить, нет ли ошибки в разряде чисел.
Пример.
Сталеалюминиевый провод АС120/19 подвешен в пролете 300 м с напряжением 13.0 даН/мм2 при температуре 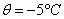 , толщине стенки гололеда
, толщине стенки гололеда 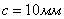 и скоростном напоре
и скоростном напоре 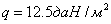 . Требуется определить стрелу провеса провода при температуре
. Требуется определить стрелу провеса провода при температуре 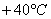 . Модуль упругости провода
. Модуль упругости провода 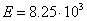 и температурный коэффициент линейного удлинения
и температурный коэффициент линейного удлинения 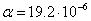 .
.
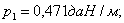
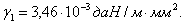
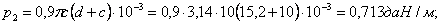
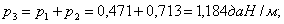
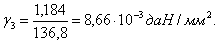
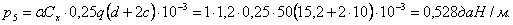
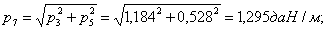
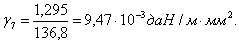
Подставляем значения в уравнение состояния провода:
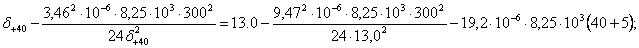
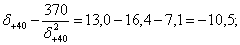
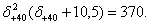 Берем по линейке значение
Берем по линейке значение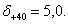 Получаем произведение
Получаем произведение
5,02 (5+10,5)=387>370. Берем меньшее значение 4,9, имеем 4,92 (4,9+10,5)=372>370.
Наконец, при 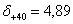 получаем точное значение произведения 4,892 (4,89+10,5)=370.
получаем точное значение произведения 4,892 (4,89+10,5)=370.
Находим стрелу провеса